9.6: Additional Calculus with Parametric and Polar

Parametric equations and polar functions expand our vision of calculus's uses. In the past few sections, we focused on this idea by differentiating and integrating parametric equations and polar functions. Now let's further extend our toolkit by discussing the following topics:

• Arc Lengths in Parametric and Polar
• Surface Areas of Revolution in Parametric and Polar

Arc Lengths in Parametric and Polar

In Section 7.1 we derived the following formula for the arc length of a smooth curve: \begin{equation} L = \int_a^b \sqrt{1 + \par{\deriv{y}{x}}^2} \di x \pd \label{eq:arc-length} \end{equation} Now let's modify this formula to be applicable to parametric equations and polar functions.

Parametric Equations Suppose that a smooth curve is parameterized by the equations \(x = f(t)\) and \(y = g(t),\) where \(\alpha \leq t \leq \beta.\) (The word smooth means \(f'\) and \(g'\) are both continuous and not simultaneously \(0\) on \(\alpha \leq t \leq \beta.\)) Then we have \(\textderiv{x}{t} = f'(t) \iffArrow\) \(\dd x = f'(t) \di t.\) Assuming \(f'(t) \ne 0,\) we have \[ \deriv{y}{x} = \frac{\textderiv{y}{t}}{\textderiv{x}{t}} = \frac{g'(t)}{f'(t)} \pd \] Replacing \(a\) with \(\alpha\) and \(b\) with \(\beta,\) and using the Substitution Rule, \(\eqref{eq:arc-length}\) becomes \begin{align} L &= \int_\alpha^\beta \sqrt{1 + \parbr{\frac{g'(t)}{f'(t)}}^2} f'(t) \di t \nonum \nl &= \int_\alpha^\beta \sqrt{\frac{[f'(t)]^2 + [g'(t)]^2}{[f'(t)]^2}} \, f'(t) \di t \nonum \nl &= \int_\alpha^\beta \frac{1}{\abs{f'(t)}} \sqrt{[f'(t)]^2 + [g'(t)]^2} \, f'(t) \di t \nonum \cma \end{align} If we assume \(f'(t) \gt 0\) on \((\alpha, \beta),\) then \(\abs{f'(t)} = f'(t)\) and thus \begin{align} L &= \int_\alpha^\beta \frac{1}{f'(t)} \sqrt{[f'(t)]^2 + [g'(t)]^2} \, f'(t) \di t \nonum \nl &= \int_\alpha^\beta \sqrt{[f'(t)]^2 + [g'(t)]^2} \di t \pd \label{eq:arc-length-parametric} \end{align} Or in Leibniz notation, we write \begin{equation} L = \int_\alpha^\beta \sqrt{\par{\deriv{x}{t}}^2 + \par{\deriv{y}{t}}^2} \di t \pd \label{eq:arc-length-para-leib} \end{equation} It turns out that \(\eqref{eq:arc-length-parametric}\) remains valid for any differentiable parametrization. We used \(f'(t) \gt 0\) as temporary technical assumption only to justify the change of variables, not to establish a requirement of the final formula.

Differentiating both parametric functions shows \[x'(t) = -4 \sin 4t \and y'(t) = 4 \cos 4t \pd\] Hence, \(\eqref{eq:arc-length-parametric}\) gives \[ \ba L &= \int_0^{\pi/2} \sqrt{(-4 \sin 4t)^2 + (4 \cos 4t)^2} \di t \nl &= \int_0^{\pi/2} \sqrt{16 \sin^2 4t + 16 \cos^2 4t} \di t \nl &= \int_0^{\pi/2} \sqrt{16 (\sin^2 4t + \cos^2 4t)} \di t \nl &= \int_0^{\pi/2} 4 \di t \nl &= 4t \intEval_0^{\pi/2} \nl &= \boxed{2 \pi} \ea \] Because the parametric equations represent a Unit Circle (Figure 1), we expect the circumference to be \(2 \pi.\)

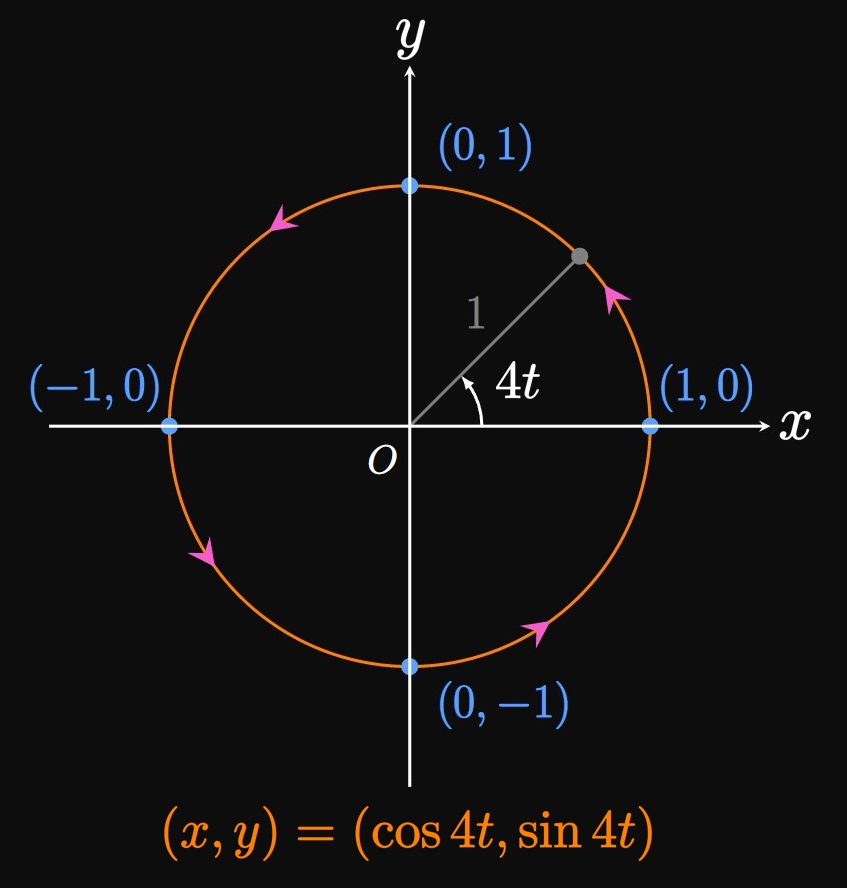
In Example 1 doubling the integral's upper bound would yield \[ \ba L &= \int_0^\pi \sqrt{(-4 \sin 4t)^2 + (4 \cos 4t)^2} \di t \nl &= \int_0^{\pi} 4 \di t = 4 \pi \pd \ea \] This result is twice the correct arc length because over \(0 \leq t \leq \pi\) the circle is traced twice, so the integral is double-counting. Therefore, ensure that the bounds traverse a parametric curve only once.

Polar Functions A polar function \(r = f(\theta)\) can be expressed parametrically as \[x = f(\theta) \cos \theta \and y = f(\theta) \sin \theta \cma\] where \(\theta\) is the parameter. Assuming that \(f'\) is continuous, let's use \(\eqref{eq:arc-length-para-leib}\) to derive a special expression for the arc length of a polar curve on \(\alpha \leq \theta \leq \beta.\) We treat \(\theta\) similarly to \(t,\) so our objective is to find an expression for \(\par{\textderiv{x}{\theta}}^2 + \par{\textderiv{y}{\theta}}^2.\) Differentiating shows \[ \ba \deriv{x}{\theta} &= f'(\theta) \cos \theta - f(\theta) \sin \theta \cma \nl \deriv{y}{\theta} &= f'(\theta) \sin \theta + f(\theta) \cos \theta \pd \ea \] Observe that \[ \ba \par{\deriv{x}{\theta}}^2 &= [f'(\theta)]^2 \cos^2 \theta - 2 f(\theta) f'(\theta) \sin \theta \cos \theta + [f(\theta)]^2 \sin^2 \theta \cma \nl \par{\deriv{y}{\theta}}^2 &= [f'(\theta)]^2 \sin^2 \theta + 2 f(\theta) f'(\theta) \sin \theta \cos \theta + [f(\theta)]^2 \cos^2 \theta \pd \ea \] Adding both equations, we get \[ \ba \par{\deriv{x}{\theta}}^2 + \par{\deriv{y}{\theta}}^2 &= [f(\theta)]^2 (\sin^2 \theta + \cos^2 \theta) + [f'(\theta)]^2 (\sin^2 \theta + \cos^2 \theta) \nl &= [f(\theta)]^2 + [f'(\theta)]^2 \cma \ea \] where the last step is true by the Pythagorean identity. Since \(r = f(\theta)\) and \(\textderiv{r}{\theta} = f'(\theta),\) we write \[[f(\theta)]^2 + [f'(\theta)]^2 = r^2 + \par{\deriv{r}{\theta}}^2 \pd\] Thus, \(\eqref{eq:arc-length-para-leib}\) gives the arc length to be \begin{equation} L = \int_\alpha^\beta \sqrt{r^2 + \par{\deriv{r}{\theta}}^2} \di \theta \pd \label{eq:arc-length-polar} \end{equation}

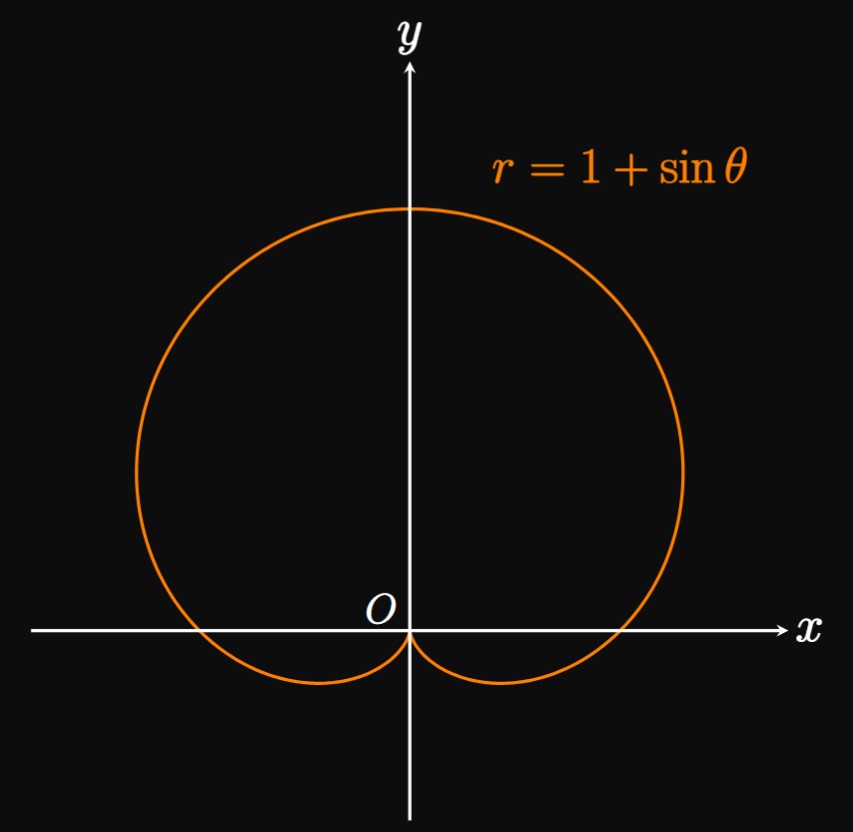
Integral Setup The graph of the cardioid is shown by Figure 2. We find \(\textderiv{r}{\theta} = \cos \theta,\) which is continuous, and \[ \ba r^2 &= (1 + \sin \theta)^2 = 1 + 2 \sin \theta + \sin^2 \theta \cma \nl \par{\deriv{r}{\theta}}^2 &= \cos^2 \theta \pd \ea \] Thus, we see \[ \ba r^2 + \par{\deriv{r}{\theta}}^2 &= 1 + 2 \sin \theta + \sin^2 \theta + \cos^2 \theta \nl &= 2 + 2 \sin \theta \pd \ea \] The entire cardioid is traced out once over \(0 \leq \theta \leq 2 \pi,\) so \(\eqref{eq:arc-length-polar}\) gives \[L = \int_0^{2 \pi} \sqrt{2 + 2 \sin \theta} \di \theta \pd\]

Evaluating the Integral We multiply the numerator and denominator inside the radical by \(2 - 2 \sin \theta,\) as follows: \[ \ba \sqrt{\par{2 + 2 \sin \theta} \par{\frac{2 - 2 \sin \theta}{2 - 2 \sin \theta}}} &= \sqrt{\frac{4 - 4 \sin^2 \theta}{2 - 2 \sin \theta}} \nl &= \sqrt{\frac{4 \cos^2 \theta}{2 - 2 \sin \theta}} \nl &= \frac{2 \abs{\cos \theta}}{\sqrt{2 - 2 \sin \theta}} \pd \ea \] The integral therefore becomes \[ \ba L &= \int_0^{2 \pi} \frac{2 \abs{\cos \theta}}{\sqrt{2 - 2 \sin \theta}} \di \theta \nl &= \int_0^{\pi/2} \frac{2 \cos \theta}{\sqrt{2 - 2 \sin \theta}} \di \theta - \int_{\pi/2}^{3\pi/2} \frac{2 \cos \theta}{\sqrt{2 - 2 \sin \theta}} \di \theta + \int_{3\pi/2}^{2\pi} \frac{2 \cos \theta}{\sqrt{2 - 2 \sin \theta}} \di \theta \cma \ea \] where the last step is true because \(\cos \theta \lt 0\) on \((\pi/2, 3\pi/2).\) To antidifferentiate \((2 \cos \theta)/\sqrt{2 - 2 \sin \theta},\) we substitute \(u = 2 - 2 \sin \theta.\) Then \(\dd u = -2 \cos \theta \di \theta,\) so we see \[ \ba \int \frac{2 \cos \theta}{\sqrt{2 - 2 \sin \theta}} \di \theta &= \int \frac{-1}{\sqrt u} \di u \nl &= -2 \sqrt{u} + C \nl &= -2 \sqrt{2 - 2 \sin \theta} + C \pd \ea \] We therefore find the arc length to be \[ \ba L &= \par{-2 \sqrt{2 - 2 \sin \theta}} \intEval_0^{\pi/2} - \par{-2 \sqrt{2 - 2 \sin \theta}} \intEval_{\pi/2}^{3\pi/2} + \par{-2 \sqrt{2 - 2 \sin \theta}} \intEval_{3\pi/2}^{2 \pi} \nl &= \par{0 + 2 \sqrt 2} - \par{-4 + 0} + \par{-2 \sqrt 2 + 4} = \boxed 8 \ea \]

Surface Areas of Revolution in Parametric and Polar

In Section 7.2 we attained the following formulas for surface areas of revolution around an axis: \begin{alignat*}{2} S &= \int_a^b 2 \pi y \di s \cma \lspace &&[\text{Rotating about } x \text{-Axis}] \nl S &= \int_c^d 2 \pi x \di s \pd \lspace &&[\text{Rotating about } y \text{-Axis}] \end{alignat*} Let's suppose that a smooth curve \(C,\) parameterized by \(x = f(t)\) and \(y = g(t),\) is revolved around the \(x\)- or \(y\)-axis. Then we modify the preceding formulas by substituting \(x = f(t)\) or \(y = g(t)\) and using the differential arc length segment \[\dd s = \sqrt{[f'(t)]^2 + [g'(t)]^2} \di t \pd\] Doing so produces the following formulas: \begin{alignat}{2} S &= \int_\alpha^\beta 2 \pi g(t) \sqrt{[f'(t)]^2 + [g'(t)]^2} \di t \cmaa g(t) \geq 0 \cma \qquad &&[\text{Rotating about } x \text{-Axis}] \label{eq:S-parametric-x} \nl S &= \int_\alpha^\beta 2 \pi f(t) \sqrt{[f'(t)]^2 + [g'(t)]^2} \di t \cmaa f(t) \geq 0 \pd \qquad &&[\text{Rotating about } y \text{-Axis}] \label{eq:S-parametric-y} \end{alignat}

The curve does not cross itself on \([0, \pi/2].\) Also observe that \[\deriv{x}{\theta} = -3 \cos^2 \theta \sin \theta \and \deriv{y}{\theta} = 3 \sin^2 \theta \cos \theta \cma\] which are both continuous. Accordingly, the differential arc length segment is \[ \ba \dd s &= \sqrt{(-3 \cos^2 \theta \sin \theta)^2 + (3 \sin^2 \theta \cos \theta)^2} \di \theta \nl &= \sqrt{9 \cos^4 \theta \sin^2 \theta + 9 \sin^4 \theta \cos^2 \theta} \di \theta \nl &= \sqrt{9 \cos^2 \theta \sin^2 \theta (\cos^2 \theta + \sin^2 \theta)} \di \theta \nl &= 3 \abs{\cos \theta \sin \theta} \di \theta = 3 \cos \theta \sin \theta \di \theta \cma \ea \] where we dropped the absolute value bars because both sine and cosine are positive on \((0, \pi/2).\) So the surface area of revolution, following \(\eqref{eq:S-parametric-x},\) is \[ \ba S &= \int_0^{\pi/2} 2 \pi \sin^3 \theta (3 \cos \theta \sin \theta) \di \theta \nl &= 6 \pi \int_0^{\pi/2} \sin^4 \theta \cos \theta \di \theta \pd \ea \] Substituting \(u = \sin \theta\) gives \(\dd u = \cos \theta \di \theta.\) When \(\theta = 0,\) \(u = 0;\) when \(\theta = \pi/2,\) \(u = 1.\) We therefore have \[ \ba S &= 6 \pi \int_0^1 u^4 \di u \nl &= \frac{6 \pi}{5} \par{u^5} \intEval_0^1 \nl &= \boxed{\frac{6 \pi}{5}} \approx 3.770 \pd \ea \] (See Figure 3.)

A similar strategy enables us to find surface areas of revolution with polar functions. By substituting \(x = f(\theta) \cos \theta\) and \(y = f(\theta) \sin \theta\) and the differential arc length segment \[\dd s = \sqrt{r^2 + \par{\deriv{r}{\theta}}^2} \di \theta = \sqrt{[f(\theta)]^2 + [f'(\theta)]^2} \cma\] we attain the following equations, assuming \(f(\theta) \geq 0 \col\) \begin{alignat}{2} S &= \small \int_\alpha^\beta 2 \pi f(\theta) \sin \theta \sqrt{[f(\theta)]^2 + [f'(\theta)]^2} \di \theta \cmaa f(\theta) \sin \theta \geq 0 \cma \qquad &&[\text{Rotating about } x \text{-Axis}] \label{eq:S-polar-x} \nl S &= \small \int_\alpha^\beta 2 \pi f(\theta) \cos \theta \sqrt{[f(\theta)]^2 + [f'(\theta)]^2} \di \theta \cmaa f(\theta) \cos \theta \geq 0 \pd \qquad &&[\text{Rotating about } y \text{-Axis}] \label{eq:S-polar-y} \end{alignat}

Observe that \(\textderiv{r}{\theta} = 2 \cos \theta,\) which is continuous, so \[ \ba r^2 + \par{\deriv{r}{\theta}}^2 &= (2 + 2 \sin \theta)^2 + (2 \cos \theta)^2 \nl &= 4 + 8 \sin \theta + 4 \sin^2 \theta + 4 \cos^2 \theta \nl &= 8 \sin \theta + 8 \cma \ea \] where the last step is true by the Pythagorean identity. The right half of the cardioid (shown in Figure 4) is traced from \(\theta = -\pi/2\) to \(\theta = \pi/2.\) We therefore use \(\eqref{eq:S-polar-y}\) to find a surface area of \[ S = 2 \pi \int_{-\pi/2}^{\pi/2} (2 + 2 \sin \theta) (\cos \theta) \sqrt{8 \sin \theta + 8} \di \theta \pd \] Substituting \(u = 8 \sin \theta + 8,\) we see \(\dd u = 8 \cos \theta \di \theta\) and \(2 + 2 \sin \theta = u/4.\) When \(\theta = -\pi/2,\) \(u = 0;\) when \(\theta = \pi/2,\) \(u = 16.\) The integral therefore becomes \[ \ba S &= \frac{\pi}{4} \int_0^{16} \par{\frac{u}{4}} \sqrt u \di u \nl &= \frac{\pi}{16} \int_0^{16} u^{3/2} \di u \nl &= \frac{\pi}{40} u^{5/2} \intEval_0^{16} \nl &= \boxed{\frac{128 \pi}{5}} \approx 80.425 \pd \ea \]